Tag Archives: VisualPatterns

Visual Patterns and Coding – Part 1 – Linear Relationships

2 Replies

Screen Shot 2015-11-30 at 12.18.45 PM.png

I have been running a ‘visual pattern’ every week with my 6th grade (pre-Algebra) classes. You can read more about this here.

To bridge the gap between pattern and function and following an online course I took with Rice University, I have started to introduce some basic coding. Python in particular. Even after one lesson of using coding and graphing, I have been able to have rich conversations about the differences between functions, input/outputs, the shape of a graph and the y-intercept. Here is the process I have taken them through:

Part 1: Have the students run through a basic (linear) visual pattern (from visualpatterns.org) using this sheet and reviewing using this slide:

Screen Shot 2015-11-30 at 12.03.09 PM.png

The nth term for this pattern is 4n+1.

Part 2: I now challenge them that we can create a calculator for this pattern using the Python coding language. I use the free python interface CodeSkulptor (from Rice University) to do this. I take them through step-by-step with some great conversations about functions and inputs/outputs.

The nice thing about CodeSkulptor is that when you hit the save button, it creates a brand new URL meaning that each student will have their own URL to post and share.

Screen Shot 2015-11-30 at 12.06.46 PM.png

They can then change the input and see clearly what happens to the output.

(Note: Lines with # are ignored by the interface)

Part 3: They then go to the Desmos Online Graphing Calculator and input the function y = 4x+1 to confirm or deny their prediction for the graph shape, from the start of the exercise. This is a great opportunity to talk about ‘step zero’ (as well as step -10 etc.) and why they graph is the shape that it is. I feel it is also important to stress the difference between 4n+1 as an nth term and y=4x+1 (which includes everything in between).

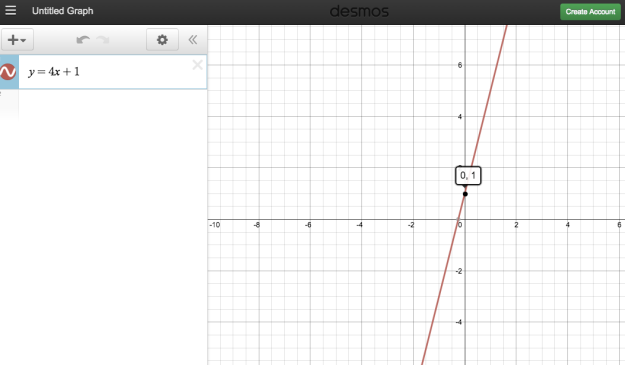
Screen Shot 2015-11-30 at 12.10.55 PM.png

Their homework is simply to follow the steps with a different (linear) visual pattern and to share their CodeSkulptor URL’s and Desmos screenshots on the class’ wiki page.

For student assistance I created this video:

Where Next?

There are two main places that I would like to take this:

  • Exponential functions
  • Inverse functions

I’m really excited about where this journey will take us. My hope is, that as these students start Algebra proper, next year, they will have a strong sense of functions graphs and their connections with patterns and geometry. Here goes…..

Have you done anything similar? I would love to hear your ideas/thoughts in the comments section, below.